금일 본 재료역학 3번은 이 것이었다.
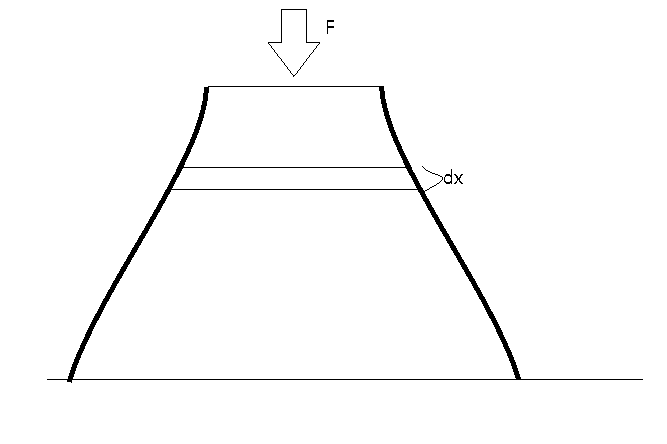
위 그림처럼 (삐뚤어지지 않은) 좌우 대칭형의 부재가 압축 하중 F를 받고 있다.
부재의 밀도는 q 이다. 부재가 처음 하중을 받는 지점(x=0)에서의 단면적을 A0 라고 할 때,
이 부재에 가해지는 축하중이 단면의 변화에 상관없이 일정하기 위한 단면적 A(x)를 구하시오
(부재의 높이는 H이다.)
이 문제를 보고 느끼길,
(1) 좌우 대칭이면 회전체 부피문제인데 왜 함수 모양이 안 주어졌을까
(2) 앞문제 풀다가 막혀서 뒤에 온 건데 이것도 못 푸네
(3) 시험 1시간 40분 남았는데 나는 진짜 개 병신인가
(4) 밤을 새서 이 과목을 공부했을 시간 동안 선형대수를 선택하였다면 적어도 한 과목은 B+ 받지 않았을까
(5) 밤을 샜는데 왜 이거 모르겠지
(6) 아 졸리네
살면서 시험을 보는 중에 집중력이 완전 흐트러져서 의도치 않게 눈 뜨고 잔 적이 이번이 처음인데,
이 문제는 어안이 벙벙하였기 때문이다.
한 축에 작용하는 변형률 가지고 일반화된 후크 법칙 이거 쓰는 거던가? -> 당연히 아니네 풀리긴 커녕 돈다 돌아
아니 y 함수가 없는데 이거 어떻게 하지?
압축 하중 F에다가 부재의 자중도 있을 것인데 이건 qVg가 될 건 분명하고 근데
dx 평판을 가지고 평형 방정식 만들 수가 있나? 이게 문제에서 위는 압축하중이고 아래론 중력인데
부재 땅바닥하고의 반력이 그 역할을 한다고 하면 이게 문제하고 무슨 상관이지? 반력은 나올 필요가 없는데
부재의 미소 성분에서도 평형이 되는 게 맞는데 아 뭔가 이상한데 내가 방향 잘못 둔 것 같네
Y(x)=Y0 + Ce^kx 으로 가정하면 어떻게 되지?
V(x) = ∫ pi( Y )^2 dx
A(x) = pi( Y )^2
변형량 문제가 아닌데 이거 이렇게 하는 게 맞나?
해서 나는 여기서 쓴 것들을 그냥 줄 찍 그어버리고 포기하였다.
근데 에타에 이 문제가 미분방정식 문제라는 것을 보고
나는 뒤통수를 심히 맞았다고 생각할 수밖에 없었다.
만일 그렇다면, Y 함수를 가정하는 게 일단 맞는 시도였을 것이고,
그 다음엔 어떻게 됐을까
부분점수라도 맞을 수 있었을까
y' 함수로 어떻게 만들어진다는 것인데
아니면 이 y 함수가 저기 부재의 겉면을 따라서 생기는 곡선 말고 다른 걸 말하는 건가?
너무 피곤하여 그냥 마친다...
벼락치기로도 아무 소용이 없는 진또배기 문제였다.
미방이 공업수학 단원 중 하나, RLC회로, 스프링, 진자 운동 모델링 문제들 중의 하나로 흘러가는 걸로 인식한 나머지
진짜로 모델링을 하는 능력을 배양하지 못한 것 같다. 이것이 벼락치기 때문에 일어난 일이라면
정말로 머리채 잡고 반성해야 할 것이다.....
'Emptiness' 카테고리의 다른 글
| 불신이 만연한 사회는 고립된 개인과 관련있다. (0) | 2019.05.18 |
|---|---|
| 휴지로 만든 껌 (0) | 2019.05.11 |
| Talk with Aristoteles of contemporary community named 'ScXXXX' at dawn (0) | 2019.05.04 |
| 이득과 손해를 감정적으로 판단하기에 (0) | 2019.05.01 |
| 고통받기 위해 사는 사람 (0) | 2019.04.30 |

